Current Status
This page documents the current status of my quest for 2LBB Busy Beavers.
Overview
The table below lists the search results for square grids for which a complete exhaustive search has been carried out. The meaning of the columns is as follows:
- Size
- The size of the program grid
- #Programs
- The total number of programs evaluated by the search
- #Hangs Detected
- The number of hangs that were automatically recognized
- #Hangs Assumed
- The number of hangs that were not automatically recognized by the current search program. These programs are assumed to be hanging because their execution exceeded a pre-configured cut-off run length
- Max Run Length
- The number of steps that the Busy Beaver (Champion) required
- Cut-off Run Length
- When the execution of program exceeds this amount of steps, it is assumed to hang. It is Not Applicable when all hanging programs are automatically detected.
- Search Time
- The time required by the search. This time varies and also depends on the machine. The reported times are for a single-threaded search on my 2.5 GHz Mac Mini.
| Size | #Programs | #Hangs Detected | #Hangs Assumed | Max Run Length | Cut-off Run Length | Search Time |
|---|---|---|---|---|---|---|
| 3×3 | 31 | 0 | 0 | 5 | N/A | 7 ms |
| 4×4 | 518 | 25 | 0 | 15 | N/A | 40 ms |
| 5×5 | 30547 | 4228 | 0 | 44 | N/A | 250 ms |
| 6×6 | 8022654 | 1546935 | 4 | 573 | 1M | 6.6 s |
| 7×7 | 11004753911 | 2501543129 | 1341811 | 97601163 | 100M | 108 h |
Hang behaviours
Table 2 shows how many programs exhibit a certain hang behavior for the various grid sizes. It distinguishes the following hang types:
- No data: A No Data Hang
- No exit: Static analysis shows that no exit can be reached from the current program state
- Periodic: A Periodic Hang stuck in a plain loop.
- Nested periodic: A Periodic Hang stuck in a nested loop.
- Regular sweep: A Sweep Hang where the sweep exhibits constant or periodic growth.
- Glider: A Glider Hang.
- A-periodic sweep: A Sweep Hang where the sweep exhibits a-periodic growth.
- Assumed: The program is assumed to hang. It does not exhibit behavior that can be detected automatically (yet).
| Hang behavior | 3x3 | 4x4 | 5x5 | 6x6 | 7x7 |
|---|---|---|---|---|---|
| No data | 0 - | 8 32.00% | 711 16.82% | 146177 9.45% | 160634153 6.42% |
| No exit | 0 - | 0 0.00% | 909 21.50% | 356882 23.07% | 548603381 21.92% |
| Periodic | 0 - | 17 68.00% | 2608 61.68% | 1036018 66.97% | 1733823991 69.27% |
| Nested periodic | 0 - | 0 0.00% | 0 0.00% | 4443 0.29% | 40347769 1.61% |
| Regular sweep | 0 - | 0 0.00% | 0 0.00% | 2453 0.16% | 13512920 0.54% |
| Glider | 0 - | 0 0.00% | 0 0.00% | 856 0.06% | 4147077 0.17% |
| A-periodic sweep | 0 - | 0 0.00% | 0 0.00% | 106 0.01% | 473838 0.02% |
| Assumed | 0 - | 0 0.00% | 0 0.00% | 4 0.00% | 1341811 0.05% |
Run length distribution
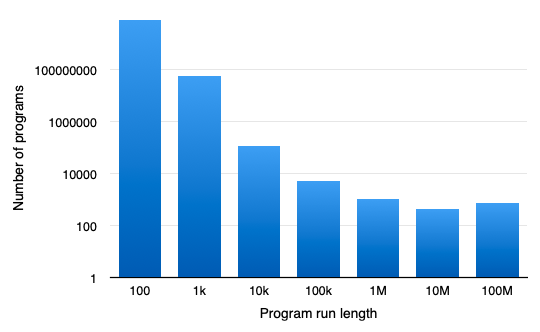
The 7×7 grid is the first where some relatively long running terminating programs exist. The longest-running program that is currently known takes more than 97.6 million steps to execute. It's interesting to see how this compares to other terminating programs. Figure 1 shows a histogram for run lengths for terminating 7×7 programs. Both axis use a logarithmic scale. The X axis shows the maximum run length for each bin. The minimum run length is one more than the maximum of the preceding bin. The height of each bar represents the number of programs in this bin. Given this distribution, one would not be surprised when there are programs that finish after more than 100 million steps.
Champions
6×6 Busy Beaver Champion
For 6×6 not all hangs are automatically detected yet. There are still four hold-outs; programs for which the search program does not yet detect that it is hanging. These, however, do not terminate without 100 million steps. Furthermore, informal analysis shows that these indeed hang. So it is very unlikely that the current Champion, with run length 573, is indeed the 6×6 Busy Beaver. This program is shown in Figure 2.
7×7 Busy Beaver Champion
For the 7×7 grid an exhaustive search has been completed with a cut-off limit of one hundred million steps. Hang detection was only enabled for the first 100000 steps. Increasing this limit lets the search detect more hangs, but slows down execution of programs that cannot (yet) be proven to hang. This search discovered a program that required 97,601,163 steps to complete. It is shown in Figure 3 and used to be the 7×7 Busy Beaver Champion.
A search is currently ongoing with a cut-off limit of one billion steps. It is expected to take about fourty days to complete. So far, it has found several programs that run for more than 100 million steps. The current 7×7 Busy Beaver Champion runs for 786,788,517 steps and is shown in Figure 4. It may be dethroned by other programs that the search is yet to visit. Watch this page.
13×13 Busy Beaver Champion
For the 13×13 grid automated search is not feasible for multiple reasons. First, there are too many possible programs. Second, their run length can be much, much longer. Third, their behavior can be much more complex. It is therefore impossible to automatically analyze all possible programs. However, it is possible to manually craft long running programs and analyze them with computer support. This way a Busy Beaver Champion has been created that runs for 2.882 × 1023409 steps. See the Discussion page for more details.